Find the cost of laying grass in a triangular field of sides 50 m, 65 m and 65 m at the rate of Rs. 7 per m2.
Thinking Process
(i) First, determine the semi-perimeter s by using formula $s=\frac{a+b+c}{2}$ and then
determine the area of a triangle by using Heron's formula $\sqrt{s(s-a)(s-b)(s-c)}$
(ii) Cost of laying grass = Area of field $\left(\right.$ in $\left.m^{2}\right) \times\left(\right.$ Cost of laying grass in $\left.1 m^{2}\right)$
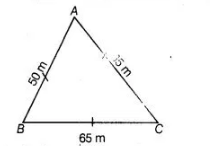
Since, $A B C$ is a triangular field of sides
$A B=a=50 m, B C=b=65 m$ and $C A=c=65 m$.
$\therefore$ Semi-perimeter of triangular field,
$s=\frac{a+b+c}{2}=\frac{50+65+65}{2}=\frac{180}{2}$
$s=90 \mathrm{~m}$
$\therefore$ Area of a triangular field
$=\sqrt{s(s-a)(s-b)(s-c)}$ [by Heron' formula]
$=\sqrt{90(90-50)(90-65)(90-65)}$
$=\sqrt{90 \times 40 \times 25 \times 25}$
$=3 \times 2 \times 10 \times 25$
$=6 \times 250=1500 \mathrm{~m}^{2}$
$\because$ Cost of laying grass per $1 \mathrm{~m}^{2}=₹ 7$
$\therefore$ Cost of laying grass per $1500 \mathrm{~m}^{2}=7 \times 1500=₹ 10500$
Hence, the cost of laying grass in a triangular field is ₹10500.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.