Find the area of the trapezium PQRS

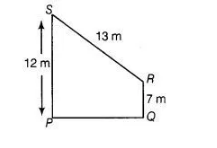
We have, trapezium $P Q R S$, in which draw a line $R T$ perpendicular to $P S$.

where, side, $S T=P S-T P=12-7=5 \mathrm{~m} .$ $[\because T P=P Q=7 \mathrm{~m}]$

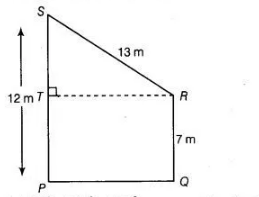
$\begin{array}{lll}\text { In right angled } \Delta S T R, & (S R)^{2}=(S T)^{2}+(T R)^{2} & \text { [by using Pythagoras theorem] }\end{array}$

$\Rightarrow \quad(13)^{2}=(5)^{2}+(T R)^{2}$

$\Rightarrow \quad(T R)^{2}=169-25$

$\Rightarrow \quad(T R)^{2}=144$

$\therefore$ $T R=12 \mathrm{~m}$

[taking positive square root because length is always positive]

Now,  area of $\Delta S T R=\frac{1}{2} \times T R \times T S$ $\left[\because\right.$ area of triangle $=\frac{1}{2}$ (base $\times$ height) $]$

$=\frac{1}{2} \times 12 \times 5=30 \mathrm{~m}^{2}$

Now, area of rectangle $P Q R T=P Q \times R Q=12 \times 7$

$[\because$ area of a rectangle $=$ length $\times$ breadth $]$

$[\because P Q=T R=12 \mathrm{~m}]$

$=84 \mathrm{~m}^{2}$

$\therefore$ Area of trapezium = Area of $D S T R+$ Area of rectangle $P Q R T$

$=30+84=114 \mathrm{~m}^{2}$

Hence, the area of trapezium is $114 \mathrm{~m}^{2}$.