Find the area of the smaller part of the circle

The area of the smaller part of the circle, $x^{2}+y^{2}=a^{2}$, cut off by the line, $x=\frac{a}{\sqrt{2}}$, is the area ABCDA.

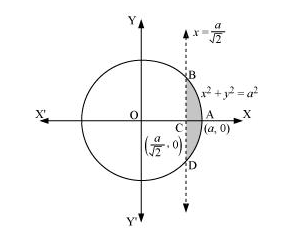
It can be observed that the area ABCD is symmetrical about x-axis.

∴ Area ABCD = 2 × Area ABC

Area of $A B C=\int_{\frac{a}{\sqrt{2}}}^{a} y d x$

$=\int_{\frac{a}{\sqrt{2}}}^{\pi} \sqrt{a^{2}-x^{2}} d x$

$=\left[\frac{x}{2} \sqrt{a^{2}-x^{2}}+\frac{a^{2}}{2} \sin ^{-1} \frac{x}{a}\right]_{\frac{a}{\sqrt{2}}}^{a}$

$=\left[\frac{a^{2}}{2}\left(\frac{\pi}{2}\right)-\frac{a}{2 \sqrt{2}} \sqrt{a^{2}-\frac{a^{2}}{2}}-\frac{a^{2}}{2} \sin ^{-1}\left(\frac{1}{\sqrt{2}}\right)\right]$

$=\frac{a^{2} \pi}{4}-\frac{a}{2 \sqrt{2}} \cdot \frac{a}{\sqrt{2}}-\frac{a^{2}}{2}\left(\frac{\pi}{4}\right)$

$=\frac{a^{2} \pi}{4}-\frac{a^{2}}{4}-\frac{a^{2} \pi}{8}$

$=\frac{a^{2}}{4}\left[\pi-1-\frac{\pi}{2}\right]$

$=\frac{a^{2}}{4}\left[\frac{\pi}{2}-1\right]$

$\Rightarrow$ Area $A B C D=2\left[\frac{a^{2}}{4}\left(\frac{\pi}{2}-1\right)\right]=\frac{a^{2}}{2}\left(\frac{\pi}{2}-1\right)$

Therefore, the area of smaller part of the circle, $x^{2}+y^{2}=a^{2}$, cut off by the line, $x=\frac{a}{\sqrt{2}}$, is $\frac{a^{2}}{2}\left(\frac{\pi}{2}-1\right)$ units.