Find the area of the shaded region in the following figure,

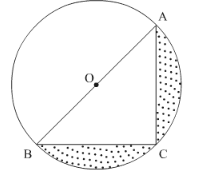
It is given a triangle ABC is cut from a circle.

$A C=24 \mathrm{~cm}$

$B C=10 \mathrm{~cm}$

Area of $\triangle A B C=\frac{1}{2} A C \times B C$

$=\frac{1}{2} \times 24 \times 10$

$=120 \mathrm{~cm}^{2}$

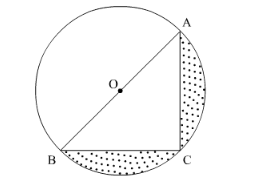
$\ln \triangle A B C$,

$\angle A C B=90^{\circ}$, Since any angle inscribed in semicircle is always right angle.

By applying Pythagoras theorem,

$A B^{2}=A C^{2}+B C^{2}$

$=24 \times 24+10 \times 10$

$=576+100$

$=676 \mathrm{~cm}^{2}$

$O A=\frac{A B}{2}$

$=\frac{26}{2} \mathrm{~cm}$

$=13 \mathrm{~cm}$

We know that the area A of circle of radius r is

$A=\pi r^{2}$

Substituting the value of radius r,

$A=3.14 \times 13 \times 13$

$=530.66 \mathrm{~cm}^{2}$

Area of semicircle $=\frac{1}{2} \pi r^{2}$

$=\frac{530.66}{2} \mathrm{~cm}^{2}$

$=265.33 \mathrm{~cm}^{2}$

Area of shaded region $=$ Area of circle $-$ Area of semicircle $-$ Area of triangle

$=530.66-265.33-120$

$=145.33 \mathrm{~cm}^{2}$