Find the area of the shaded region in fig. below

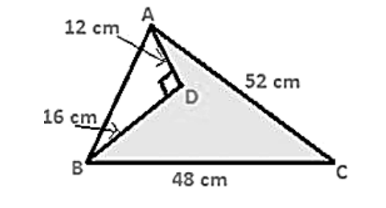
Area of the shaded region = Area of ΔABC − Area of ΔADB

Now in triangle ADB

$\mathrm{AB}^{2}=\mathrm{AD}^{2}+\mathrm{BD}^{2} \ldots .$ (i)

Given, AD = 12 cm, BD =16 cm

Substituting the value of AD and BD in eq (i), we get

$A B^{2}=12^{2}+16^{2}$

$=400 \mathrm{~cm}^{2}$

AB = 20 cm

Now, area of a triangle = 1/2 × AD × BD

$=96 \mathrm{~cm}^{2}$

Now in triangle ABC,

S =1/2 × (AB + BC + CA)

= 1/2 × (52 + 48 + 20)

= 60 cm

By using Heron's Formula

The area of a triangle $=\sqrt{s \times(s-a) \times(s-b) \times(s-c)}$

$=\sqrt{60 \times(60-20) \times(60-48) \times(60-52)}$

$=480 \mathrm{~cm}^{2}$

Thus, the area of a triangle is $480 \mathrm{~cm}^{2}$

Area of shaded region = Area of triangle ABC - Area of triangle ADB

$=(480-96) \mathrm{cm}^{2}$

$=384 \mathrm{~cm}^{2}$

Area of shaded region $=384 \mathrm{~cm}^{2}$