Find the area of the region lying in the first quadrant and bounded by

The area in the first quadrant bounded by $y=4 x^{2}, x=0, y=1$, and $y=4$ is represented by the shaded area $\mathrm{ABCDA}$ as

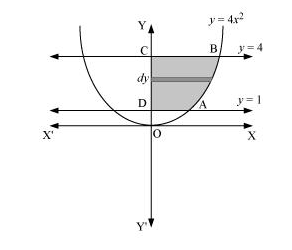
Area of $\mathrm{ABCDA}=\int_{1}^{4} x d y$

$=\int_{1}^{4} \frac{\sqrt{y}}{2} d y \quad\left[\right.$ as, $\left.y=4 x^{2}\right]$

$=\frac{1}{2} \int_{1}^{4} \sqrt{y} d y$

$=\frac{1}{2} \times \frac{2}{3}\left[y^{3 / 2}\right]_{1}^{4}$

$=\frac{1}{3}\left[(4)^{3 / 2}-(1)^{3 / 2}\right]$

$=\frac{1}{3}(8-1)$

$=\frac{1}{3} \times 7$

$=\frac{7}{3}$ square units