Find the area of the quadrilaterals, the coordinates of whose vertices are

(i)

Let the vertices of the quadrilateral be A (−3, 2), B (5, 4), C (7, −6), and D (−5, −4). Join AC to form two triangles ΔABC and ΔACD.

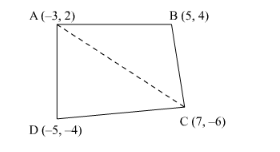
Area of a triangle $=\frac{1}{2}\left\{x_{1}\left(y_{2}-y_{3}\right)+x_{2}\left(y_{3}-y_{1}\right)+x_{3}\left(y_{1}-y_{2}\right)\right\}$

Area of $\triangle \mathrm{ABC}=\frac{1}{2}\{-3(4+6)+5(-6-2)+7(2-4)\}$

$=\frac{1}{2}(-30-40-14)=-42$

$\therefore$ Area of $\triangle \mathrm{ABC}=42$ square units

Area of $\Delta \mathrm{ACD}=\frac{1}{2}\{-3(-6+4)+7(-4-2)-5(2+6)\}$

$=\frac{1}{2}\{6-42-40\}=-38$

$\therefore$ Area of $\triangle \mathrm{ACD}=38$ square units

Area of $\square \mathrm{ABCD}=$ Area of $\triangle \mathrm{ABC}+$ Area of $\triangle \mathrm{ACD}$

$=(42+38)$ square units $=80$ square units

(ii)

Let the vertices of the quadrilateral be A (1, 2), B (6, 2), C (5, 3), and D (3, 4). Join AC to form two triangles ΔABC and ΔACD.

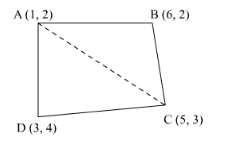
Area of a triangle $=\frac{1}{2}\left\{x_{1}\left(y_{2}-y_{3}\right)+x_{2}\left(y_{3}-y_{1}\right)+x_{3}\left(y_{1}-y_{2}\right)\right\}$

Area of $\triangle \mathrm{ABC}=\frac{1}{2}\{1(2-3)+6(3-2)+5(2-2)\}$

$=\frac{1}{2}(-1+6)=\frac{5}{2}$ square units

Area of $\triangle \mathrm{ACD}=\frac{1}{2}\{1(3-4)+5(4-2)+3(2-3)\}$

$=\frac{1}{2}\{-1+10-3\}=3$ square units

Area of $\square \mathrm{ABCD}=$ Area of $\triangle \mathrm{ABC}+$ Area of $\triangle \mathrm{ACD}$

$=\left(\frac{5}{2}+3\right)$ square units $=\frac{11}{2}$ square units

(iii)

Let the vertices of the quadrilateral be A (−4, −2), B (−3, −5), C (3, −2), and D (2, 3). Join AC to form two triangles ΔABC and ΔACD.

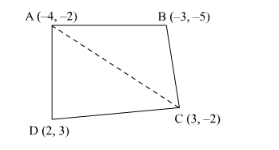
Area of a triangle $=\frac{1}{2}\left\{x_{1}\left(y_{2}-y_{3}\right)+x_{2}\left(y_{3}-y_{1}\right)+x_{3}\left(y_{1}-y_{2}\right)\right\}$

Area of $\triangle \mathrm{ABC}=\frac{1}{2}[(-4)\{(-5)-(-2)\}+(-3)\{(-2)-(-2)\}+3\{(-2)-(-5)\}]$

$=\frac{1}{2}(12+0+9)=\frac{21}{2}$ square units

Area of $\triangle \mathrm{ACD}=\frac{1}{2}[(-4)\{(-2)-(3)\}+3\{(3)-(-2)\}+2\{(-2)-(-2)\}]$

$=\frac{1}{2}\{20+15+0\}=\frac{35}{2}$ square units

Area of $\square \mathrm{ABCD}=$ Area of $\triangle \mathrm{ABC}+$ Area of $\triangle \mathrm{ACD}$

$=\left(\frac{21}{2}+\frac{35}{2}\right)$ square units $=28$ square units