Find the area of the quadrilateral ABCD in which AD = 24 cm, ∠BAD = 90°

∆">∆BDC is an equilateral triangle with side a= 26 cm.

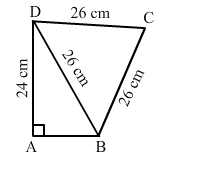
Area of $\Delta B D C=\frac{\sqrt{3}}{4} a^{2}$

$=\frac{\sqrt{3}}{4} \times 26^{2}$

$=\frac{1.73}{4} \times 676$

$=292.37 \mathrm{~cm}^{2}$

By using Pythagoras' theorem in the right-angled triangle $\triangle D A B$, we get:

$A D^{2}+A B^{2}=B D^{2}$

$\Rightarrow 24^{2}+A B^{2}=26^{2}$

$\Rightarrow A B^{2}=26^{2}-24^{2}$

$\Rightarrow A B^{2}=676-576$

$\Rightarrow A B^{2}=100$

$\Rightarrow A B=10 \mathrm{~cm}$

Area of $\Delta A B D=\frac{1}{2} \times b \times h$

$=\frac{1}{2} \times 10 \times 24$

$=120 \mathrm{~cm}^{2}$

Area of the quadrilateral $=$ Area of $\triangle B C D+$ Area of $\triangle A B D$

$=292.37+120$

$=412.37 \mathrm{~cm}^{2}$

Perimeter of the quadrilateral = AB + BC + CD + AD

= 24 + 10 + 26 + 26

= 86 cm