Find the area of a trapezium whose parallel sides are 11 ma and 25 m long, and the nonparallel sides are 15 m and 13 m long.
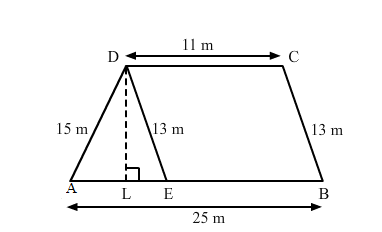
Draw $D E \| B C$ and $D L$ perpendicular to $A B$.
The opposite sides of quadrilateral DEBC are parallel. Hence, DEBC is a parallelogram.
∴ DE = BC = 13 m
Also
$A E=(A B-E B)=(A B-D C)=(25-11)=14 \mathrm{~m}$
For $\Delta D A E$
Let:
AE = a =14 m
DE = b = 13 m
DA = c =15 m
Thus, we have:
$s=\frac{a+b+c}{2}$
$s=\frac{14+13+15}{2}=21 \mathrm{~m}$
Area of $\Delta D A E=\sqrt{s(s-a)(s-b)(s-c)}$
$=\sqrt{21 \times(21-14)} \times(21-13) \times(21-15)$
$=\sqrt{21 \times 7 \times 8 \times 6}$
$=\sqrt{7056}$
$=84 \mathrm{~m}^{2}$
Area of $\Delta D A E=\frac{1}{2} \times A E \times D L$
$\Rightarrow 84=\frac{1}{2} \times 14 \times D L$
$\Rightarrow \frac{84 \times 2}{14}=D L$
$\Rightarrow D L=12 \mathrm{~m}$
Area of trapezium $=\frac{1}{2} \times($ Sum of parallel sides $) \times($ Distance between them $)$
$=\frac{1}{2} \times(11+25) \times 12$
$=\frac{1}{2} \times 36 \times 12$
$=216 \mathrm{~m}^{2}$
