Find the area of a trapezium whose parallel sides are 11 m and 25 m long,

In the given figure, ABCD is the trapezium.

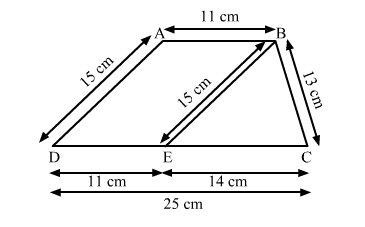
Draw a line BE parallel to AD.

In ∆BCE,
The sides of the triangle are of length 15 m, 13 m and 14 m.
∴ Semi-perimeter of the triangle is

$s=\frac{15+13+14}{2}=\frac{42}{2}=21 \mathrm{~m}$

∴ By Heron's formula,

Area of $\Delta B C E=\sqrt{s(s-a)(s-b)(s-c)}$

$=\sqrt{21(21-15)(21-13)(21-14)}$

$=\sqrt{21(6)(8)(7)}$

$=84 \mathrm{~m}^{2} \quad \ldots(1)$

Also,

Area of $\Delta B C E=\frac{1}{2} \times$ Base $\times$ Height

$\Rightarrow 84=\frac{1}{2} \times 14 \times$ Height

$\Rightarrow 84=7 \times$ Height

$\Rightarrow$ Height $=\frac{84}{7}$

$\Rightarrow$ Height $=12 \mathrm{~m}$

∴ Height of ∆BCE = Height of the parallelogram ABED = 12 m

Now,
Area of the parallelogram ABED = Base × Height
 = 11 × 12
 = 132 m2                     ...(2)

∴ Area of the trapezium = Area of the parallelogram ABED + Area of the triangle BCE
= 132 + 84
= 216 m2

Hence, the area of a trapezium is 216 m2.