Find the area of a trapezium whose parallel sides are 11 cm

We will divide the trapezium into a triangle and a parallelogram.

Difference in the lengths of parallel sides $=25-11=14 \mathrm{~cm}$

We can represent this in the following figure:

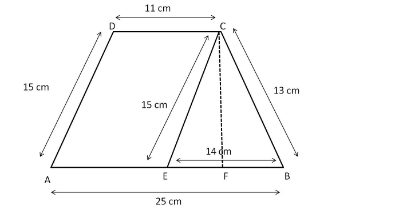
Trapezium ABCD is divided into parallelogram AECD and triangle CEB.

1.Consider triangle CEB.

In triangle CEB, we have:

$E B=25-11=14 \mathrm{~cm}$

Using Hero's theorem, we will first evaluate the semiperimeter of triangle CEB and then evaluate its area.

Semiperimeter, $s=\frac{1}{2}(a+b+c)=\frac{1}{2}(15+13+14)=\frac{42}{2}=21 \mathrm{~cm}$

Area of triangle $C E B=\sqrt{s(s-a)(s-b)(s-c)}$ $=\sqrt{21(21-15)(21-13)(21-14)}$

$=\sqrt{21 \times 6 \times 8 \times 7}$

$=\sqrt{7056}$

$=84 \mathrm{~cm}^{2}$

Also,

Area of triangle $C E B=\frac{1}{2}($ Base $\times$ Height $)$

Height of triangle $C E B=\frac{\text { Area } \times 2}{\text { Base }}=\frac{84 \times 2}{14}=12 \mathrm{~cm}$

2. Consider parallelogram $A E C D$.

Area of parallelogram $A E C D=$ Height $\times$ Base $=A E \times C F=12 \times 11=132 \mathrm{~cm}^{2}$

Area of trapezium $A B C D=\operatorname{Ar}(\Delta B E C)+\operatorname{Ar}($ parallelogram $A E C D)=132+84=216 \mathrm{~cm}^{2}$