Find the area of a rhombus whose perimeter is 80 m and one of whose diagonal is 24 m.

Solution:

Given,

Perimeter of a rhombus = 80 m

As we know,

Perimeter of a rhombus = 4 × side = 4 × a

4 × a = 80 m

a = 20 m

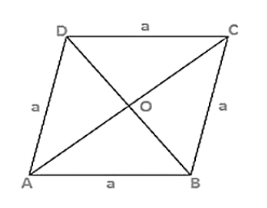
Let AC = 24 m

Therefore OA = 1/2 × AC

OA = 12 m

In triangle AOB

$\mathrm{OB}^{2}=\mathrm{AB}^{2}-\mathrm{OA}^{2}$

$\mathrm{OB}^{2}=20^{2}-12^{2}$

OB = 16 m

Also, OB = OD because diagonal of rhombus bisect each other at 90°

Therefore, BD = 2 OB = 2 × 16 = 32 m

Area of rhombus = 1/2 × BD × AC

Area of rhombus = 1/2 × 32 × 24

Area of rhombus $=384 \mathrm{~m}^{2}$