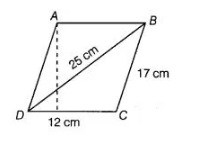
Find the area of a parallelogram given in the figure.

Solution:

Area of parallelogram $\quad A B C D=2$ (Area of $\triangle B C D$ ) $\ldots(\mathrm{i})$

Now, the sides of a $\triangle B C D$ are $a=12 \mathrm{~cm}, b=17 \mathrm{~cm}$ and $c=25 \mathrm{~cm}$.

$\therefore \quad$ Semi-perimeter of $\triangle B C D, s=\frac{a+b+c}{2}=\frac{12+17+25}{2}=\frac{54}{2}=27 \mathrm{~cm}$

$\therefore \quad$ Area of $\triangle B C D=\sqrt{s(s-a)(s-b)(s-c)} \quad$ [by Heron's formula]

$=\sqrt{27(27-12)(27-17)(27-25)}$

$=\sqrt{27 \times 15 \times 10 \times 2}$

$=\sqrt{9 \times 3 \times 3 \times 5 \times 5 \times 2 \times 2}$

 

=3 x 3 x 5 x 2 cm2

Area of parallelogram ABCD = 2 x 90

= 180 cm2 …(ii)

Let altitude of a parallelogram be h.

Also, area of parallelogram ABCD =Base x Altitude

=> 180 = DC x h [from Eq. (ii)]

=> 180 = 12 x h

∴ h = 180/12= 15 cm

Hence, the area of parallelogram is 180 cm2 and the length of altitude is 15 cm.