Find the area enclosed between the parabola

The area enclosed between the parabola, $y^{2}=4 a x$, and the line, $y=m x$, is represented by the shaded area $\mathrm{OABO}$ as

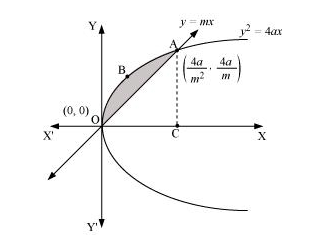
The points of intersection of both the curves are $(0,0)$ and $\left(\frac{4 a}{m^{2}}, \frac{4 a}{m}\right)$.

We draw AC perpendicular to x-axis.

∴ Area OABO = Area OCABO – Area (ΔOCA)

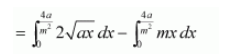
$=2 \sqrt{a}\left[\frac{x^{\frac{3}{2}}}{\frac{3}{2}}\right]_{0}^{\frac{4 a}{m^{2}}}-m\left[\frac{x^{2}}{2}\right]_{0}^{\frac{4 a}{m^{2}}}$

$=\frac{4}{3} \sqrt{a}\left(\frac{4 a}{m^{2}}\right)^{\frac{3}{2}}-\frac{m}{2}\left[\left(\frac{4 a}{m^{2}}\right)^{2}\right]$

$=\frac{32 a^{2}}{3 m^{3}}-\frac{m}{2}\left(\frac{16 a^{2}}{m^{4}}\right)$

$=\frac{32 a^{2}}{3 m^{3}}-\frac{8 a^{2}}{m^{3}}$

$=\frac{8 a^{2}}{3 m^{3}}$ units