Express each of the following product as a monomials and verify the result for x = 1, y = 2:

To multiply algebraic expressions, we use commutative and associative laws along with the laws of indices, i.e., $a^{m} \times a^{n}=a^{m+n}$.

We have:

$\left(\frac{1}{8} x^{2} y^{4}\right) \times\left(\frac{1}{4} x^{4} y^{2}\right) \times(x y) \times 5$

$=\left(\frac{1}{8} \times \frac{1}{4} \times 5\right) \times\left(x^{2} \times x^{4} \times x\right) \times\left(y^{4} \times y^{2} \times y\right)$

$=\left(\frac{1}{8} \times \frac{1}{4} \times 5\right) \times\left(x^{2+4+1}\right) \times\left(y^{4+2+1}\right)$

$=\frac{5}{32} x^{7} y^{7}$

To verify the result, we substitute x = 1 and y = 2 in LHS; we get:

$\mathrm{LHS}=\left(\frac{1}{8} x^{2} y^{4}\right) \times\left(\frac{1}{4} x^{4} y^{2}\right) \times(x y) \times 5$

$=\left\{\frac{1}{8} \times(1)^{2} \times(2)^{4}\right\} \times\left\{\frac{1}{4} \times(1)^{4} \times(2)^{2}\right\} \times(1 \times 2) \times 5$

$=\left(\frac{1}{8} \times 1 \times 16\right) \times\left(\frac{1}{4} \times 1 \times 4\right) \times(1 \times 2) \times 5$

$=2 \times 1 \times 2 \times 5$

$=20$

Substituting x = 1 and y = 2 in RHS, we get:​

$\mathrm{RHS}=\frac{5}{32} x^{7} y^{7}$

$=\frac{5}{32}(1)^{7}(2)^{7}$

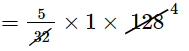
= 20

Because LHS is equal to RHS, the result is correct.

Thus, the answer is $\frac{5}{32} x^{7} y^{7}$.