Evaluate $\int \tan ^{3} \mathrm{x} \mathrm{dx}$
$\int \tan ^{3} x d x$
We can write above integral as:
$\int \tan ^{3} x d x=\int\left(\tan ^{2} x\right)(\tan x) d x \cdots\left(\right.$ Splitting $\left.\tan ^{3} x\right)$
$=\int\left(\sec ^{2} x-1\right)(\tan x) d x\left(U \operatorname{sing} \tan ^{2} x=\sec ^{2} x-1\right)$
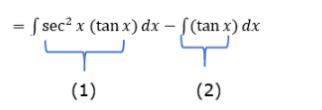
Considering integral (1)
Let $u=\tan x$
$d u=\sec ^{2} x d x$
Substituting values we get,
$\int \sec ^{2} x(\tan x) d x=\int u d u=\frac{u^{2}}{2}+C$
Substituting value of $u$ we get,
$\int \sec ^{2} x(\tan x) d x=\frac{\tan ^{2} x}{2}+C$
$\therefore$ integral becomes,
$\int \sec ^{2} x(\tan x) d x-\int(\tan x) d x=\frac{\tan ^{2} x}{2}-\int(\tan x) d x$
$=\frac{\tan ^{2} x}{2}-(-\log |\cos x|)+C\left[\because \int \tan x d x=-\log |\cos x|+C\right]$
$\therefore \int \tan ^{3} x d x=\frac{\tan ^{2} x}{2}+\log |\cos x|+C$
