Each side of a rhombus is 10 cm long and one of its diagonals measures 16 cm.

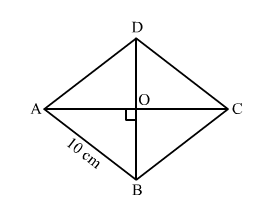
Let $A B C D$ be a rhombus.

$\therefore A B=B C=C D=D A=10 \mathrm{~cm}$

Let $A C$ and $B D$ be the diagonals of $A B C D$. Let $A C=x$ and $B D=16 \mathrm{~cm}$ and $\mathrm{O}$ be the intersection point of the diagonals.

We know that the diagonals of a rhombus are perpendicular bisectors of each other.

$\therefore \triangle A O B$ is a right angle triangle, in which $O A=A C \div 2=x \div 2$ and $O B=B D \div 2=16 \div 2=8 \mathrm{~cm}$.

Now, $A B^{2}=O A^{2}+O B^{2}$  [Pythagoras theorem]

$\Rightarrow 10^{2}=\left(\frac{x}{2}\right)^{2}+8^{22}$

$\Rightarrow 100-64=\frac{x^{2}}{4}$

$\Rightarrow 36 \times 4=x$

$\Rightarrow x^{2}=144$

∴ x = 12 cm

Hence, the other diagonal of the rhombus is 12 cm.

$\therefore$ Area of the rhombus $=\frac{1}{2} \times(12 \times 16)=96 \mathrm{~cm}^{2}$