E is the mid-point of a median AD of ΔABC

Given In a $\triangle A B C, A D$ is a median and $E$ is the mid-point of $A D$. Construction Draw DP $\| E F$.

Proof In $\triangle A D P, E$ is the mid-point of $A D$ and $E F \| D P$.

So, $F$ is mid-point of $A P$. [by converse of mid-point theorem]

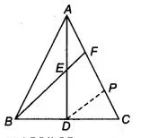
In $\Delta F B C, D$ is mid-point of $B C$ and $D P \| B F$.

So, $P$ is mid-point of $F C$.

Thus, $A F=F P=P C$

$\therefore$ $A F=\frac{1}{3} A C$

Hence proved.