Draw the graph of the linear equation 3x + 4y = 6.

The given equation is $3 x+4 y=6$. To draw the graph of this equation, we need atleast two points lying on the graph of

$4 y=6-3 x$

$\Rightarrow$ $y=\frac{6-3 x}{4}$

When $x=2$, then $y=\frac{6-3 \times 2}{4}=\frac{6-6}{4}=0$

When $x=0$, then $y=\frac{6-3 \times 0}{4}=\frac{6}{4}=\frac{3}{2}$

Here, we find two points $A\left(0, \frac{3}{2}\right)$ and $B(2,0)$.

Now, plot the points $A\left(0, \frac{3}{2}\right)$ and $B(2,0)$ and join them, to get the line $A B$. Line $A B$ is the required graph.

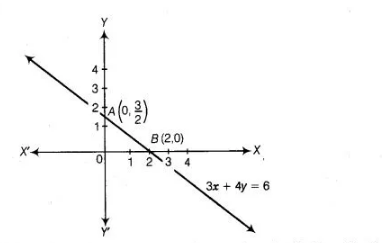
You can see that the graph (line $A B$ ) cuts the $X$-axis at the point $(2,0)$ and the $Y$-axis at the point $\left(0, \frac{3}{2}\right)$