Question.
Diagonals $A C$ and $B D$ of a quadrilateral $A B C D$ intersect each other at $P .$ Show that $\operatorname{ar}(A P B) \times \operatorname{ar}(C P D)=\operatorname{ar}(A P D) \times \operatorname{ar}(B P C)$
Solution:
Let us draw $A M \perp B D$ and $C N \perp B D$
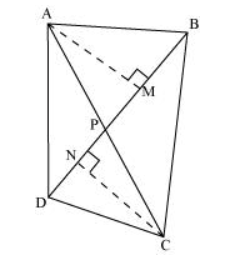
Area of a triangle $=\frac{1}{2} \times$ Base $\times$ Altitude
$\operatorname{ar}(\mathrm{APB}) \times \operatorname{ar}(\mathrm{CPD})=\left[\frac{1}{2} \times \mathrm{BP} \times \mathrm{AM}\right] \times\left[\frac{1}{2} \times \mathrm{PD} \times \mathrm{CN}\right]$
$=\frac{1}{4} \times \mathrm{BP} \times \mathrm{AM} \times \mathrm{PD} \times \mathrm{CN}$
$\operatorname{ar}(\mathrm{APD}) \times \operatorname{ar}(\mathrm{BPC})=\left[\frac{1}{2} \times \mathrm{PD} \times \mathrm{AM}\right] \times\left[\frac{1}{2} \times \mathrm{CN} \times \mathrm{BP}\right]$
$=\frac{1}{4} \times \mathrm{PD} \times \mathrm{AM} \times \mathrm{CN} \times \mathrm{BP}$
$=\frac{1}{4} \times \mathrm{BP} \times \mathrm{AM} \times \mathrm{PD} \times \mathrm{CN}$
$\therefore \operatorname{ar}(\mathrm{APB}) \times \operatorname{ar}(\mathrm{CPD})=\operatorname{ar}(\mathrm{APD}) \times \operatorname{ar}(\mathrm{BPC})$
Let us draw $A M \perp B D$ and $C N \perp B D$

Area of a triangle $=\frac{1}{2} \times$ Base $\times$ Altitude
$\operatorname{ar}(\mathrm{APB}) \times \operatorname{ar}(\mathrm{CPD})=\left[\frac{1}{2} \times \mathrm{BP} \times \mathrm{AM}\right] \times\left[\frac{1}{2} \times \mathrm{PD} \times \mathrm{CN}\right]$
$=\frac{1}{4} \times \mathrm{BP} \times \mathrm{AM} \times \mathrm{PD} \times \mathrm{CN}$
$\operatorname{ar}(\mathrm{APD}) \times \operatorname{ar}(\mathrm{BPC})=\left[\frac{1}{2} \times \mathrm{PD} \times \mathrm{AM}\right] \times\left[\frac{1}{2} \times \mathrm{CN} \times \mathrm{BP}\right]$
$=\frac{1}{4} \times \mathrm{PD} \times \mathrm{AM} \times \mathrm{CN} \times \mathrm{BP}$
$=\frac{1}{4} \times \mathrm{BP} \times \mathrm{AM} \times \mathrm{PD} \times \mathrm{CN}$
$\therefore \operatorname{ar}(\mathrm{APB}) \times \operatorname{ar}(\mathrm{CPD})=\operatorname{ar}(\mathrm{APD}) \times \operatorname{ar}(\mathrm{BPC})$
