Determine, graphically whether the system of equations x − 2y = 2, 4x − 2y = 5 is consistent or in-consistent.

The given equations are

$x-2 y=2$$\ldots(i)$

$4 x-2 y=5$....(ii)

Putting $x=0$ in equation $(i)$, we get:

$\Rightarrow 0-2 y=2$

$\Rightarrow y=-1$

$\Rightarrow x=0, \quad y=-1$

Putting $y=0$ in equation $(i)$ we get:

$\Rightarrow x-2 \times 0=2$

$\Rightarrow x=2$

$\Rightarrow x=2, \quad y=0$

Use the following table to draw the graph.

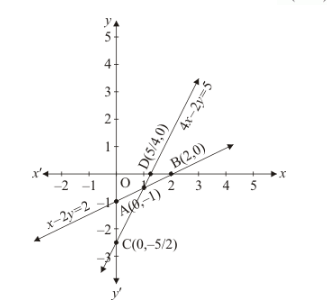
Draw the graph by plotting the two points $A(0,-1), B(2,0)$ from table.

$4 x-2 y=5$...(ii)

Putting $x=0$ in equation (ii) we get:

$\Rightarrow 4 \times 0-2 y=5$

$\Rightarrow y=-5 / 2$

$\Rightarrow x=0, \quad y=-5 / 2$

Putting $y=0$ in equation $(i i)$, we get:

$\Rightarrow 4 x-2 \times 0=5$

$\Rightarrow x=5 / 4$

$\Rightarrow x=5 / 4, \quad y=0$

Use the following table to draw the graph.

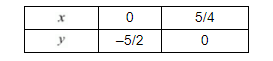
Draw the graph by plotting the two points $C(0,-5 / 2), D(5 / 4,0)$ from table.

It has unique solution.

Hence the system of equations is consistent