Question:
D is any point on side AC of a ΔABC with AB = AC. Show that CD < BD.
Solution:
Given in $\triangle A B C, D$ is any point on side $A C$ such that $A B=A C$. To show $C DC D$.
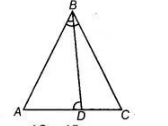
Proof In $\triangle A B C$, $A C=A B$ [qiven]
$\Rightarrow$ $\angle A B C=\angle A C B$ ...(i)
[angles opposite to equal sides are equal]
In $\triangle A B C$ and $\triangle D B C$, $\angle A B C>\angle D B C$ [since, $\angle D B C$ is a internal angle of $\angle B$ ]
$\Rightarrow$ $\angle A C B>\angle D B C$ [from Eq. (i)]
$\Rightarrow$ $B D>C D$ [side opposite to greater angle is longer]
or $C D
