Question.
D, E and F are respectively the mid-points of the sides BC, CA and AB of a ΔABC. Show that
(i) BDEF is a parallelogram.
(ii) $\operatorname{ar}(D E F)=\frac{1}{4} \operatorname{ar}(A B C)$
(iii) $\operatorname{ar}(\mathrm{BDEF})=\frac{1}{2} \operatorname{ar}(\mathrm{ABC})$
D, E and F are respectively the mid-points of the sides BC, CA and AB of a ΔABC. Show that
(i) BDEF is a parallelogram.
(ii) $\operatorname{ar}(D E F)=\frac{1}{4} \operatorname{ar}(A B C)$
(iii) $\operatorname{ar}(\mathrm{BDEF})=\frac{1}{2} \operatorname{ar}(\mathrm{ABC})$
Solution:
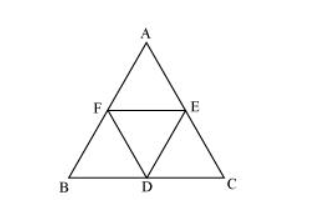
(i) $\ln \triangle A B C$,
$E$ and $F$ are the mid-points of side $A C$ and $A B$ respectively.
Therefore, $E F \| B C$ and $E F=\frac{1}{2} B C$ (Mid-point theorem)
However, $B D=\frac{1}{2} B C(D$ is the mid-point of $B C)$
Therefore, $B D=E F$ and $B D \| E F$
Therefore, BDEF is a parallelogram.
(ii) Using the result obtained above, it can be said that quadrilaterals BDEF, DCEF, AFDE are parallelograms.
We know that diagonal of a parallelogram divides it into two triangles of equal area.
$\therefore$ Area $(\Delta B F D)=$ Area $(\Delta D E F)($ For parallelogram BD $)$
Area (ΔCDE) = Area (ΔDEF) (For parallelogram DCEF)
Area (ΔAFE) = Area (ΔDEF) (For parallelogram AFDE)
$\therefore$ Area $(\triangle \mathrm{AFE})=$ Area $(\triangle \mathrm{BFD})=$ Area $(\triangle \mathrm{CDE})=$ Area $(\triangle \mathrm{DEF})$
Also,
Area $(\Delta \mathrm{AFE})+$ Area $(\Delta \mathrm{BDF})+$ Area $(\Delta \mathrm{CDE})+$ Area $(\Delta \mathrm{DEF})=$ Area $(\triangle \mathrm{ABC})$
$\Rightarrow$ Area $(\Delta \mathrm{DEF})+$ Area $(\Delta \mathrm{DEF})+$ Area $(\Delta \mathrm{DEF})+$ Area $(\Delta \mathrm{DEF})=$ Area $(\Delta \mathrm{ABC})$
$\Rightarrow 4$ Area $(\triangle \mathrm{DEF})=$ Area $(\triangle \mathrm{ABC})$
$\Rightarrow$ Area $(\Delta \mathrm{DEF})=\frac{1}{4}$ Area $(\triangle \mathrm{ABC})$
(iii) Area (parallelogram BDEF) = Area ( $\triangle \mathrm{DEF})+$ Area ( $\triangle \mathrm{BDF}$ )
$\Rightarrow$ Area $($ parallelogram BDEF $)=$ Area $(\triangle D E F)+$ Area $(\triangle D E F)$
$\Rightarrow$ Area (parallelogram BDEF) $=2$ Area ( $\triangle \mathrm{DEF}$ )
$\Rightarrow$ Area (parallelogram BDEF) $=2 \times \frac{1}{4}$ Area ( $\triangle \mathrm{ABC}$ )
$\Rightarrow$ Area (parallelogram BDEF) $=\frac{1}{2}$ Area ( $\left.\triangle \mathrm{ABC}\right)$

(i) $\ln \triangle A B C$,
$E$ and $F$ are the mid-points of side $A C$ and $A B$ respectively.
Therefore, $E F \| B C$ and $E F=\frac{1}{2} B C$ (Mid-point theorem)
However, $B D=\frac{1}{2} B C(D$ is the mid-point of $B C)$
Therefore, $B D=E F$ and $B D \| E F$
Therefore, BDEF is a parallelogram.
(ii) Using the result obtained above, it can be said that quadrilaterals BDEF, DCEF, AFDE are parallelograms.
We know that diagonal of a parallelogram divides it into two triangles of equal area.
$\therefore$ Area $(\Delta B F D)=$ Area $(\Delta D E F)($ For parallelogram BD $)$
Area (ΔCDE) = Area (ΔDEF) (For parallelogram DCEF)
Area (ΔAFE) = Area (ΔDEF) (For parallelogram AFDE)
$\therefore$ Area $(\triangle \mathrm{AFE})=$ Area $(\triangle \mathrm{BFD})=$ Area $(\triangle \mathrm{CDE})=$ Area $(\triangle \mathrm{DEF})$
Also,
Area $(\Delta \mathrm{AFE})+$ Area $(\Delta \mathrm{BDF})+$ Area $(\Delta \mathrm{CDE})+$ Area $(\Delta \mathrm{DEF})=$ Area $(\triangle \mathrm{ABC})$
$\Rightarrow$ Area $(\Delta \mathrm{DEF})+$ Area $(\Delta \mathrm{DEF})+$ Area $(\Delta \mathrm{DEF})+$ Area $(\Delta \mathrm{DEF})=$ Area $(\Delta \mathrm{ABC})$
$\Rightarrow 4$ Area $(\triangle \mathrm{DEF})=$ Area $(\triangle \mathrm{ABC})$
$\Rightarrow$ Area $(\Delta \mathrm{DEF})=\frac{1}{4}$ Area $(\triangle \mathrm{ABC})$
(iii) Area (parallelogram BDEF) = Area ( $\triangle \mathrm{DEF})+$ Area ( $\triangle \mathrm{BDF}$ )
$\Rightarrow$ Area $($ parallelogram BDEF $)=$ Area $(\triangle D E F)+$ Area $(\triangle D E F)$
$\Rightarrow$ Area (parallelogram BDEF) $=2$ Area ( $\triangle \mathrm{DEF}$ )
$\Rightarrow$ Area (parallelogram BDEF) $=2 \times \frac{1}{4}$ Area ( $\triangle \mathrm{ABC}$ )
$\Rightarrow$ Area (parallelogram BDEF) $=\frac{1}{2}$ Area ( $\left.\triangle \mathrm{ABC}\right)$
