D, E and F are respectively the mid-points

Given In a ΔABC, D, E and F are respectively the mid-points of the sides AB, BC and CA. To prove ΔABC is divided into four congruent triangles.

Proof Since, ABC is a triangle and D, E and F are the mid-points of sides AB, BC and CA, respectively.

Then, $\quad A D=B D=\frac{1}{2} A B, B E=E C=\frac{1}{2} B C$

and $A F=C F=\frac{1}{2} A C$

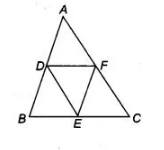
Now, using the mid-point theorem,

$E F \| A B$ and $E F=\frac{1}{2} A B=A D=B D$

$E D \| A C$ and $E D=\frac{1}{2} A C=A F=C F$

and 

$A F=C F=\frac{1}{2} A C$

Now, using the mid-point theorem,

$E F \| A B$ and $E F=\frac{1}{2} A B=A D=B D$

$E D \| A C$ and $E D=\frac{1}{2} A C=A F=C F$

and 

$D F \| B C$ and $D F=\frac{1}{2} B C=B E=C E$

In $\triangle A D F$ and $\triangle E F D$, $A D=E F$

$A F=D E$

and $D F=F D$ [common]

$\begin{array}{lll}\therefore & \Delta A D F \equiv \Delta E F D & \text { [by SSS congruence rule] }\end{array}$

Similarty, $\triangle D E F \equiv \triangle E D B$

and $\triangle D E F \cong \triangle C F E$

So, $\triangle A B C$ is divided into four congruent triangles.

Hence proved.