Copper reduces $\mathrm{NO}_{3}^{-}$into $\mathrm{NO}$ and $\mathrm{NO}_{2}$ depending upon the concentration of $\mathrm{HNO}_{3}$ in solution. (Assuming fixed $\left[\mathrm{Cu}^{2+}\right]$ and $\mathrm{P}_{\mathrm{NO}}=\mathrm{P}_{\mathrm{NO}_{2}}$ ), the $\mathrm{HNO}_{3}$ concentration at which the thermodynamic tendency for reduction of $\mathrm{NO}_{3}^{-}$into $\mathrm{NO}$ and $\mathrm{NO}_{2}$ by copper is same is $10^{x} \mathrm{M}$. The value of $2 x$ is_________________(Rounded-off to the nearest integer)
$\left[\right.$ Given, $\mathrm{E}_{\mathrm{Cu}^{2+} / \mathrm{Cu}}^{\mathrm{o}}=0.34 \mathrm{~V}, \mathrm{E}_{\mathrm{NO}_{3}^{-} / \mathrm{NO}}^{\circ}=0.96 \mathrm{~V}$
$\mathrm{E}_{\mathrm{NO}_{3}^{-} / \mathrm{NO}_{2}}^{\mathrm{o}}=0.79 \mathrm{~V}$ and at $298 \mathrm{~K}$
$\left.\frac{\mathrm{RT}}{\mathrm{F}}(2.303)=0.059\right]$
If the partial pressure of $\mathrm{NO}$ and $\mathrm{NO}_{2}$ gas is taken as 1 bar, then Answer is 4, else the question is bonus.
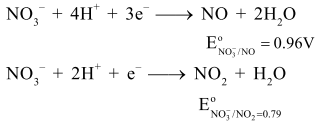
Let $\left[\mathrm{HNO}_{3}\right]=\mathrm{y} \Rightarrow\left[\mathrm{H}^{+}\right]=\mathrm{y}$ and $\left[\mathrm{NO}_{3}^{-}\right]=\mathrm{y}$ for same thermodynamic tendency
$\mathrm{E}_{\mathrm{NO}_{3}^{-} / \mathrm{NO}}=\mathrm{E}_{\mathrm{NO}_{3}^{-} / \mathrm{NO}_{2}}$
or, $\mathrm{E}_{\mathrm{NO}_{3}^{-} / \mathrm{No}}^{\mathrm{o}}-\frac{0.059}{3} \log \frac{\mathrm{P}_{\mathrm{NO}}}{\mathrm{y} \times \mathrm{y}^{4}}$
$=\mathrm{E}_{\mathrm{NO}_{3}^{-} / \mathrm{NO}_{2}}^{\mathrm{o}}-\frac{0.059}{1} \log \frac{\mathrm{P}_{\mathrm{NO}_{2}}}{\mathrm{y} \times \mathrm{y}^{2}}$
or, $0.96-\frac{0.059}{3} \log \frac{\mathrm{P}_{\mathrm{NO}}}{\mathrm{y}^{5}}=0.79-\frac{0.059}{1} \log \frac{\mathrm{P}_{\mathrm{NO}_{2}}}{\mathrm{y}^{3}}$
or, $0.17=-\frac{0.059}{1} \log \frac{\mathrm{P}_{\mathrm{NO}_{2}}}{\mathrm{y}^{3}}+\frac{0.059}{3} \log \frac{\mathrm{P}_{\mathrm{NO}}}{\mathrm{y}^{5}}$
$0.17=-\frac{0.0591}{1} \log \frac{\mathrm{P}_{\mathrm{NO}_{2}}}{\mathrm{y}^{3}}+\frac{0.0591}{3} \log \frac{\mathrm{P}_{\mathrm{NO}}}{\mathrm{y}^{5}}$
$0.17=-\frac{0.0591}{3} \log \frac{\mathrm{P}_{\mathrm{NO}_{2}}^{3}}{\mathrm{y}^{9}}+\frac{0.0591}{3} \log \frac{\mathrm{P}_{\mathrm{NO}}}{\mathrm{y}^{5}}$
$0.17=\frac{0.0591}{3}\left[\log \frac{\mathrm{P}_{\mathrm{NO}}}{\mathrm{y}^{5}}-\log \frac{\mathrm{P}_{\mathrm{NO}_{2}}^{3}}{\mathrm{y}^{9}}\right]$
$0.17=\frac{0.0591}{3}\left[\log \frac{\mathrm{P}_{\mathrm{NO}}}{\mathrm{y}^{5}} \times \frac{\mathrm{y}^{9}}{\mathrm{P}_{\mathrm{NO}_{2}}^{3}}\right]$
Assume $\mathrm{P}_{\mathrm{NO}} \simeq \mathrm{P}_{\mathrm{NO}_{2}}=1 \mathrm{bar}$
$\frac{0.17 \times 3}{0.059}=\log \mathrm{y}^{4}=8.644$
$\log \mathrm{y}=\frac{8.644}{4}$
$\log \mathrm{y}=2.161$
$y=10^{2.16}$
$\therefore 2 x=2 \times 2.161=4.322$
Answer (4)
