Construct each of the following angles, using ruler and compasses:

(i) 75°
Steps of construction
1. Draw a line XY.
2. Take a point O on XY. 
3. With O as centre, draw a semi circle, cutting XY at P and Q.

4. Construct $\angle Y O R=90^{\circ}$.

5. Draw the bisector of $\angle Y O R=90^{\circ}$ cutting the semi circle at point $S$.

6. With $S$ and $T$ as centres draw two arcs intersecting at point $A$.

$\angle \mathrm{AOY}=75^{\circ}$

(ii) 37.5°

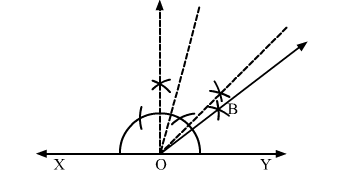
Steps of construction
1. Draw a line XY.
2. Take a point O on XY. 
3. With O as centre, draw a semi circle, cutting XY at P and Q.

4. Construct $\angle \mathrm{YOR}=90^{\circ}$.

5. Draw the bisector of $\angle Y O R=90^{\circ}$ cutting the semi circle at point $S$.

6. With S and T as centres draw two arcs intersecting at point A. 
7. Draw the angle bisector of ∠">∠AOY. 
8. ∠">∠BOY is the required angle of  37.5°. 

(iii) 135°

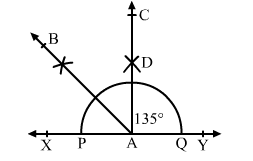
Steps of construction:
1. Draw a line XY.
2. Take a point A on XY.
3. With A as centre, draw a semi circle, cutting XY at P and Q.
4. Construct ∠">∠YAC = 90°">°°.
5. Draw $A B$, bisector of $\angle X A C$.

Thus, $\angle Y A B=135^{\circ}$

(iv) 105°

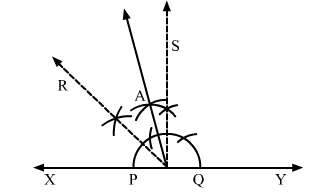
Steps of construction

1. Draw a line XY.
2. Take a point O on XY.
3. With O as centre, draw a semi circle, cutting XY at P and Q.

4. Construct $\angle \mathrm{YOS}=90^{\circ}$.

5. Draw $\mathrm{RO}$, bisector of $\angle \mathrm{XOS}$.

6. Draw AO, bisector of $\angle \mathrm{ROS}$.

$\angle \mathrm{AOY}=105^{\circ}$ is the required angle.

(v) 22.5°

Steps of construction:
1. Draw a ray AB.

2. Draw an angle $\angle B A E=45^{\circ}$.

3. With A as the centre and a small radius, draw an arc cutting AB at P and AE at Q.
4. With P as the centre and a radius more than half of PQ, draw an arc.
5. With Q as the centre and the same radius as above, draw another arc cutting the previously drawn arc at D.
6. Join AD.

Thus, $\angle B A C$ is the required angle of measure $22.5^{\circ}$.