Construct a triangle with sides $5 \mathrm{~cm}, 6 \mathrm{~cm}$ and $7 \mathrm{~cm}$ and then another triangle whose sides are$\frac{\mathbf{7}}{\mathbf{5}}$ of the corresponding sides of the first triangle.
Steps of Construction :
1. Construct a $\triangle \mathrm{ABC}$ such that $\mathrm{AB}=5 \mathrm{~cm}$,
$\mathrm{BC}=7 \mathrm{~cm}$ and $\mathrm{AC}=6 \mathrm{~cm}$
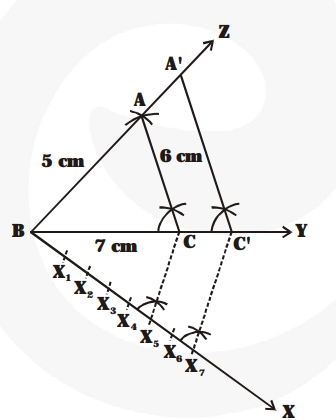
2. Draw a ray $\mathrm{BX}$ such that $\angle \mathrm{CBX}$ is an acute angle.
3. Mark 7 points $X_{1}, X_{2}, X_{3}, X_{4}, X_{5}, X_{6}$ and $X_{7}$ on $B X$ such that $B X_{1}=X_{1} X_{2}=X_{2} X_{3}=X_{3} X_{4}$ $=X_{4} X_{5}=X_{5} X_{6}=X_{6} X_{7}$
4. Join $X_{5}$ to $C$.
5. Draw a line through $X_{7}$ intersecting $B C$ (produced) at $C^{\prime}$ such that $X_{5} C \| X_{7} C^{\prime}$
6. Draw a line through $\mathrm{C}^{\prime}$ parallel to $\mathrm{CA}$ to intersect $\mathrm{BA}$ (produced) at $\mathrm{A}^{\prime}$.
Thus, $\triangle \mathrm{A}^{\prime} \mathrm{BC}^{\prime}$ is the required triangle.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.