Construct a triangle whose sides are 3.6 cm ,

To construct a triangle $A B C$ in which $A B=3.6 \mathrm{~cm}, A C=3.0 \mathrm{~cm}$ and $B C=4.8 \mathrm{~cm}$, use the following steps.

1. Draw a line segment $B C$ of length $4.8 \mathrm{~cm}$.

2. From B, point A is at a distance of $3.6 \mathrm{~cm}$. So, having B as centre, draw an arc of radius $3.6 \mathrm{~cm}$.

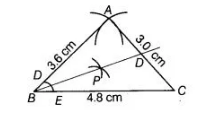
3. From $\mathrm{C}$, point $\mathrm{A}$ is at a distance of $3 \mathrm{~cm}$. So, having $\mathrm{C}$ as centre, draw an arc of radius $3 \mathrm{~cm}$ which intersect previous arc at $\mathrm{A}$.

4. Join $A B$ and $A C$. Thus, $\triangle A B C$ is the required triangle.

Flere, angle B is smallest, as AC is the smallest side. To direct angle B, we use the following steps.

1. Taking B as centre, we draw an are intersecting AB and BC at D and E, respectively.

2. Taking $D$ and $E$ as centres we draw arcs intersecting at $P$.

3. Joining BP, we obtain angle bisector of $\angle B$.

4. Flere, $\angle A B C=39^{\circ}$

Thus, $\angle A B D=\angle D B C=1 / 2 \times 139^{\circ}=19.5^{\circ}$