Construct a triangle similar to a given ΔXYZ with its sides equal to (3/4)th of the corresponding

Solution:

Given that

Construct a $\triangle X Y Z$ of given data, Let $X Y=5 \mathrm{~cm}, Y Z=6 \mathrm{~cm}$ and $\angle Y=60^{\prime}$ and then a triangle similar to it whose sides are $(3 / 4)$ of the corresponding sides of $\triangle X Y Z$.

We follow the following steps to construct the given

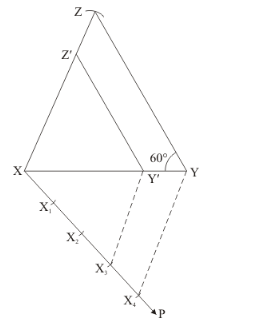
Step of construction

Step: I- First of all we draw a line segment $X Y=5 \mathrm{~cm}$.

Step: II- With $Y$ as centre draw an angle $\angle Y=60^{\circ}$.

Step: III- With $Y$ as centre and radius $=Y Z=6 \mathrm{~cm}$, draw an arc.

Step: IV-Join $X Z$ to obtain $\triangle X Y Z$.

 

Step: V-Below $X Y$, makes an acute angle $\angle Y X P=60^{\circ}$.

Step: VI -Along $X P$, mark off four points $X_{1}, X_{2} X_{3}$ and $X_{4}$ such that $X X_{1}=X_{1} X_{2}=X_{2} X_{3}=X_{3} X_{4}$

Step: VII- Join $X_{4} Y$.

Step: VIII- Since we have to construct a triangle each of whose sides is $(3 / 4)^{\text {th }}$ of the corresponding sides of $\triangle X Y Z$.

So, we take three parts out of four equal parts on $X P$ from point $X_{3}$ draw $X_{3} Y^{\prime} \| X_{4} Y$, and meeting $X Y$ at $Y^{\prime}$.

Step: IX- From $Y^{\prime}$ draw $Y^{\prime} Z^{\prime} \| Y Z$, and meeting $X Z$ at $Z^{\prime}$

 

Thus, $\triangle X Y^{\prime} Z^{\prime}$ is the required triangle, each of whose sides is $(3 / 4)^{\text {th }}$ of the corresponding sides of $\triangle X Y Z$.