Construct a rhombus whose side is of length

We know that, in rhombus all sides are equal. To construct a rhombus whose side is of length $3.4 \mathrm{~cm}$ and one of its angle is $45^{\circ}$, use the following steps

1. Draw a line segment AS of length $3.4 \mathrm{~cm}$.

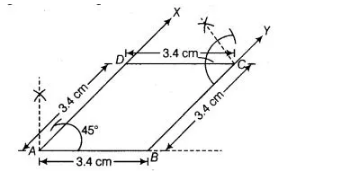
2. Now, generate an angle $45^{\circ}$ at both ends $A$ and $B$ of line segment $A B$ and plot the parallel lines $A X$ and BY.

3. Cut $A D$ and $S C$ of length $3.4 \mathrm{~cm}$ from $A X$ and $B Y$, respectively.

4. Draw an angle of $45^{\circ}$ at one of the point $D$ or $C$ and join both points by a line segment $D C$ of length $3.4$ $\mathrm{cm}$ and parallel to $\mathrm{AB}$.

Thus, $A B C D$ is the required rhombus whose side is of length $3.4 \mathrm{~cm}$ and one of its angle is $45^{\circ}$.

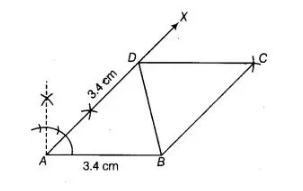
Alternate Method

To construct a rhombus whose side is of length $3.4 \mathrm{~cm}$ and one of its angle is $45^{\circ}$, use the following steps.

1. Draw a line segment $A B$ of length $3.4 \mathrm{~cm}$.

2. Now, draw an angle $X A B=45^{\circ}$ at point $A$ of line segment $A B$.

3. Cut a line segment $A D=3.4 \mathrm{~cm}$ from the ray $A X$ and join $B D$.

4. Now, from $D$ point $C$ is at a distance of $3.4 \mathrm{~cm}$. So, having $D$ as centre draw an arc of radius $3.4 \mathrm{~cm}$.

5. From $B$, point $C$ is at distance of $3.4 \mathrm{~cm}$. So, having $B$ as centre draw an arc of radius $3.4 \mathrm{~cm}$ which intersect previous arc (obtained in step iv) at $C$.

6. Join $C D$ and $B C$.

Thus, $A B C D$ is required rhombus whose side is of length $3.4 \mathrm{~cm}$ and one of its angle is $45^{\circ}$.