Construct a $\triangle \mathrm{PQR}$, in which $\mathrm{PQ}=6 \mathrm{~cm}, \mathrm{QR}=7 \mathrm{~cm}$ and $\mathrm{PR}=8 \mathrm{~cm}$. Then, construct another triangle whose sides are $\frac{4}{5}$ times the corresponding sides of $\triangle \mathrm{PQR}$.
Steps of Construction
Step 1. Draw a line segment QR = 7 cm.
Step 2. With Q as centre and radius 6 cm, draw an arc.
Step 3. With R as centre and radius 8 cm, draw an arc cutting the previous arc at P.
Step 4. Join PQ and PR. Thus, ∆PQR is the required triangle.
Step 5 . Below $Q R$, draw an acute angle $\angle R Q X$.
Step 6. Along QX, mark five points R1, R2, R3, R4 and R5 such that QR1 = R1R2 = R2R3 = R3R4 = R4R5.
Step 7. Join RR5.
Step 8. From R4, draw R4R' || RR5 meeting QR at R'.
Step 9. From R', draw P'R' || PR meeting PQ in P'.
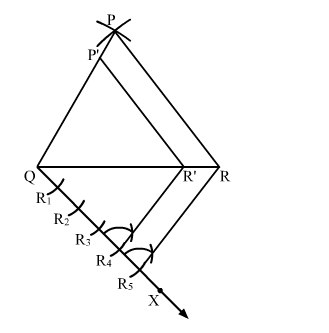
Here, $\triangle \mathrm{P}^{\prime} \mathrm{QR}^{\prime}$ is the required triangle, each of whose sides are $\frac{4}{5}$ times the corresponding sides of $\triangle \mathrm{PQR}$.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.