Question:
Consider the two sets :
$A=\left\{m \in \mathbf{R}:\right.$ both the roots of $x^{2}-(m+1) x+m+4=0$
are real $\}$ and $B=[-3,5)$.
Which of the following is not true?
Correct Option: 1
Solution:
$A=\left\{m \in \mathbf{R}: x^{2}-(m+1) x+m+4=0\right.$ has real roots $\}$
$D \geq 0$
$\Rightarrow(m+1)^{2}-4(m+4) \geq 0$
$\Rightarrow m^{2}-2 m-15 \geq 0$
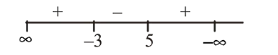
$A=\{(-\infty,-3] \cup[5, \infty)\}$
$B=[-3,5) \Rightarrow A-B=(-\infty,-3) \cup[5, \infty)$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.