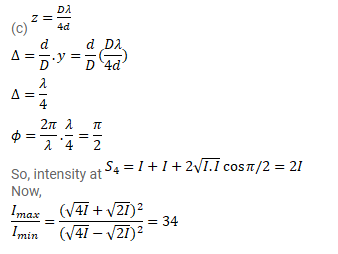Question:
Consider the situation given in the figure. The two slits $\mathrm{S}_{1}$ and $\mathrm{S}_{2}$ placed symmetrically around the central line are illuminated by a monochromatic light of wavelength $\lambda$. The separation between the slits is $d$. The light transmitted by the slits falls on a screen $\Sigma_{1}$ placed at a distance $D$ from the slits. The slit $S_{3}$ is at the central line and the slit $S_{4}$ is at a distance $z$ from $S_{3}$ Another screen $\Sigma_{2}$ is placed a further distance $D$ away from $\Sigma_{1}$. Find the ratio of the maximum to minimum intensity observed on $\Sigma_{2}$ if $z$ is equal to
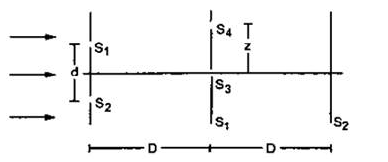
(a) $z=\frac{\lambda D}{2 d},(\mathrm{~b}) \frac{\lambda D}{d},(\mathrm{c}) \frac{\lambda D}{4 d}$
Solution: