Question:
Consider the following frequency distribution :
$\begin{array}{lccccc}\text { Class: } & 0-6 & 6-12 & 12-18 & 18-24 & 24-30 \\ \text { Frequency: } & \text { a } & \text { b } & 12 & 9 & 5\end{array}$
If mean $=\frac{309}{22}$ and median $=14$, then the value $(a-b)^{2}$ is equal to
Solution:

Mean $=\frac{3 a+9 b+180+189+135}{a+b+26}=\frac{309}{22}$
$\Rightarrow 66 a+198 b+11088=309 a+309 b+8034$
$\Rightarrow 243 a+111 b=3054$
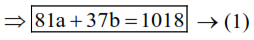
Now, Median $=12+\frac{\frac{\mathrm{a}+\mathrm{b}+26}{2}-(\mathrm{a}+\mathrm{b})}{12} \times 6=14$
$\Rightarrow \frac{13}{2}-\left(\frac{a+b}{4}\right)=2$
$\Rightarrow \frac{a+b}{4}=\frac{9}{2}$
$\Rightarrow \frac{\mathrm{a}+\mathrm{b}}{4}=\frac{9}{2}$
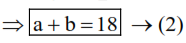
From equation (1) \& (2)
$a=8, b=10$
$\therefore(a-b)^{2}=(8-10)^{2}$
