Consider the binary operations*: $\mathbf{R} \times \mathbf{R} \rightarrow$ and $0: \mathbf{R} \times \mathbf{R} \rightarrow \mathbf{R}$ defined as $a * b=|a-b|$ and $a \circ b=a, \& m n$ ForE; $a, b \in \mathbf{R}$. Show that * is commutative but not associative, o is associative but not commutative. Further, show that \&mnForE; $a, b, c \in \mathbf{R}, a^{\star}(b$ o $c)=\left(a^{*} b\right) \circ\left(a^{*} c\right) .$ [If it is so, we say that the operation * distributes over the operation o]. Does o distribute over *? Justify your answer.
It is given that ${ }^{*}: \mathbf{R} \times \mathbf{R} \rightarrow$ and $0: \mathbf{R} \times \mathbf{R} \rightarrow \mathbf{R}$ isdefined as
$a * b=|a-b|$ and $a$ o $b=a$, \&mnForE; $a, b \in \mathbf{R}$.
For $a, b \in \mathbf{R}$, we have:
$a * b=|a-b|$
$b * a=|b-a|=|-(a-b)|=|a-b|$
∴a * b = b * a
∴ The operation * is commutative.
It can be observed that,
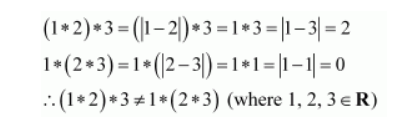
$\therefore$ The operation * is not associative.
Now, consider the operation o:
It can be observed that $102=1$ and $201=2$.
$\therefore 1 \circ 2 \neq 2 \circ 1$ (where $1.2 \in \mathbf{R}$ )
∴The operation o is not commutative.
Let $a, b, c \in \mathbf{R}$. Then, we have:
$(a \circ b) \circ c=a \circ c=a$
$a \circ(b \circ c)=a \circ b=a$
$\Rightarrow a \circ b) \circ c=a \circ(b \circ c)$
$\therefore$ The operation o is associative.
Now, let $a, b, c \in \mathbf{R}$, then we have:
$a^{\star}(b \circ c)=a^{\star} b=|a-b|$
$\left(a^{*} b\right) \circ\left(a^{*} c\right)=(|a-b|) \circ(|a-c|)=|a-b|$
Hence, $a^{*}(b \circ c)=\left(a^{*} b\right) \circ\left(a^{*} c\right) .$
Now,
$1 \circ(2 * 3)=1 \circ(|2-3|)=1 \circ 1=1$
$(1 \circ 2)^{*}(1 \circ 3)=1^{*} 1=|1-1|=0$
$\therefore 1 \circ\left(2^{*} 3\right) \neq(1 \circ 2)^{*}(1 \circ 3)($ where $1,2,3 \in \mathbf{R})$
The operation o does not distribute over *.