Question:
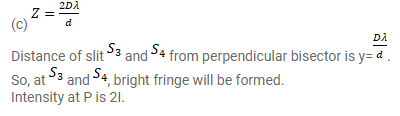
Consider the arrangement shown in figure. By some mechanism, the separation between the slits $\mathrm{S}_{3}$ and $\mathrm{S}_{4}$ can be changed. The intensity is measured at the point $\mathrm{P}$ which is common perpendicular bisector of $\mathrm{S}_{1} \mathrm{~S}_{2}$ and $\mathrm{S}_{3} \mathrm{~S}_{4}$. When $z=\frac{D \lambda}{2 d}$, the intensity measured at $P$ is $I$. Find this intensity when $z$ is equal to
(a) $\frac{D \lambda}{2 d},(\mathrm{~b})^{\frac{3 D \lambda}{2 d}}$, (c) $\frac{2 D \lambda}{d}$
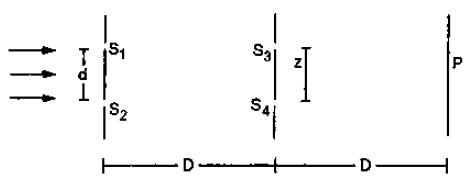
Solution: