Question:
Consider $f: \mathbf{R}_{+} \rightarrow[-5, \infty)$ given by $f(x)=9 x^{2}+6 x-5 .$ Show that $f$ is invertible with $f^{-1}(y)=\left(\frac{(\sqrt{y+6})-1}{3}\right)$
Solution:
$f: \mathbf{R}_{+} \rightarrow[-5, \infty)$ is given as $f(x)=9 x^{2}+6 x-5$
Let $y$ be an arbitrary element of $[-5, \infty)$.
Let $y=9 x^{2}+6 x-5$
$\Rightarrow y=(3 x+1)^{2}-1-5=(3 x+1)^{2}-6$
$\Rightarrow(3 x+1)^{2}=y+6$
$\Rightarrow 3 x+1=\sqrt{y+6} \quad[$ as $y \geq-5 \Rightarrow y+6>0]$
$\Rightarrow x=\frac{\sqrt{y+6}-1}{3}$
$\therefore f$ is onto, thereby range $f=[-5, \infty)$.
Let us define $g:[-5, \infty) \rightarrow \mathbf{R}_{+}$as $g(y)=\frac{\sqrt{y+6}-1}{3}$.
We now have:
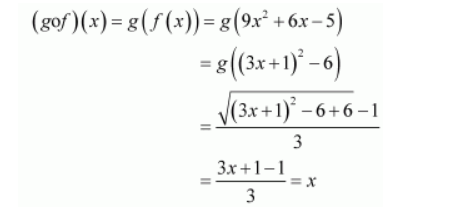
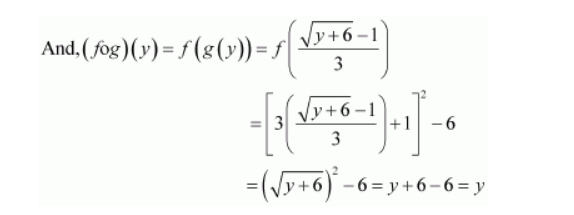
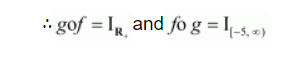
Hence, f is invertible and the inverse of f is given by
$f^{-1}(y)=g(y)=\frac{\sqrt{y+6}-1}{3} .$
