Consider a triangular plot $\mathrm{ABC}$ with sides $\mathrm{AB}=7 \mathrm{~m}, \mathrm{BC}=5 \mathrm{~m}$ and $\mathrm{CA}=6 \mathrm{~m}$. A vertical lamp-post at the mid point $\mathrm{D}$ of $\mathrm{AC}$ subtends an angle $30^{\circ}$ at $\mathrm{B}$. The height (in $\mathrm{m}$ ) of the lamp-post is:
Correct Option: , 2
Let the height of the lamp-post is $h$.
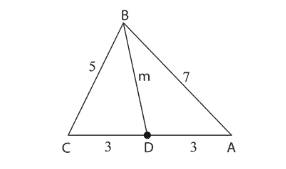
By Appolonius Theorem,
$2\left(B D^{2}+\left(\frac{A C}{2}\right)^{2}\right)=B C^{2}+A B^{2}$
$\Rightarrow 2\left(m^{2}+3^{2}\right)=25+49 \Rightarrow m=2 \sqrt{7}$
$\tan 30^{\circ}=\frac{h}{B D}$
$\Rightarrow h=2 \sqrt{7} \times \frac{1}{\sqrt{3}}=\frac{2 \sqrt{21}}{3}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.