Question:
Consider a triangle having vertices $\mathrm{A}(-2,3), \mathrm{B}(1,9)$ and $\mathrm{C}(3,8)$. If a line $\mathrm{L}$ passing through the circum-centre of triangle $A B C$, bisects line $B C$, and intersects $\mathrm{y}$-axis at point $\left(0, \frac{\alpha}{2}\right)$, then the value of real number $\alpha$ is
Solution:
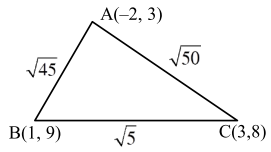
$(\sqrt{50})^{2}=(\sqrt{45})^{2}+(\sqrt{5})^{2}$
$\angle \mathrm{B}=90^{\circ}$
Circum-center $=\left(\frac{1}{2}, \frac{11}{2}\right)$
Mid point of $\mathrm{BC}=\left(2, \frac{17}{2}\right)$
Line : $\left(y-\frac{11}{2}\right)=2\left(x-\frac{1}{2}\right) \Rightarrow y=2 x+\frac{9}{2}$
Passing though $\left(0, \frac{\alpha}{2}\right)$
$\frac{\alpha}{2}=\frac{9}{2} \Rightarrow \alpha=9$
