Compare the modal ages of two groups of students appearing for an entrance test:

Solution:

For group “A”

The maximum frequency is 78 so the modal class is 18–20.

Therefore,

$l=18$

$h=2$

$f=78$

$f_{1}=50$

 

$f_{2}=46$

$\Rightarrow$ Mode $=l+\frac{f-f_{1}}{2 f-f_{1}-f_{2}} \times h$

$=18+\frac{78-50}{156-50-46} \times 2$

$=18+\frac{14}{15}$

$=18+0.93$

Mode $=18.93$

For group “B”

The maximum frequency 89 so modal class 18–20.

Therefore,

$l=18$

$h=2$

$f=89$

$f_{1}=54$

 

$f_{2}=40$

$\Rightarrow$ Mode $=18+\frac{89-54}{178-54-40} \times 2$

$=18+\frac{35}{84} \times 2$

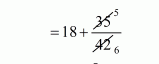
$=18+\frac{5}{6}$

$=18+0.83$

Mode $=18.83$

Thus, the modal age of group A is 18.93 years whereas the modal age of group B is 18.83 years.