Choose the correct answer of the following question:

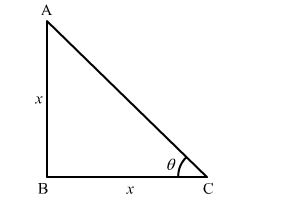
Let AB represents the vertical pole and BC represents the shadow on the ground and θ represents angle of elevation the sun.

In $\triangle \mathrm{ABC}$,

$\tan \theta=\frac{\mathrm{AB}}{\mathrm{BC}}$

$\Rightarrow \tan \theta=\frac{x}{x} \quad(\mathrm{As}$, the height of the pole, $\mathrm{AB}=$ the length of the shadow, $\mathrm{BC}=x)$

$\Rightarrow \tan \theta=1$

$\Rightarrow \tan \theta=\tan 45^{\circ}$

$\therefore \theta=45^{\circ}$

Hence, the correct answer is option (c).