Choose the correct answer of the following question:

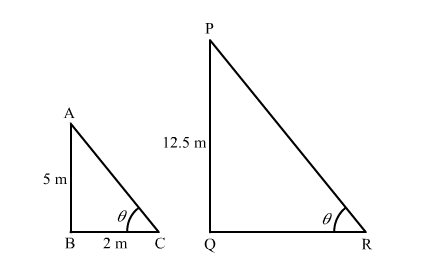
Let AB be a stick and BC be its shadow; and PQ be the tree and QR be its shadow.

We have,

$\mathrm{AB}=5 \mathrm{~m}, \mathrm{BC}=2 \mathrm{~m}, \mathrm{PQ}=12.5 \mathrm{~m}$

In $\Delta \mathrm{ABC}$,

$\tan \theta=\frac{\mathrm{AB}}{\mathrm{BC}}$

$\Rightarrow \tan \theta=\frac{5}{2} \quad \ldots \ldots(\mathrm{i})$

Now, in $\Delta \mathrm{PQR}$,

$\tan \theta=\frac{\mathrm{PQ}}{\mathrm{QR}}$

$\Rightarrow \frac{5}{2}=\frac{12.5}{Q R} \quad[$ Using (i) $]$

$\Rightarrow \mathrm{QR}=\frac{12.5 \times 2}{5}=\frac{25}{5}$

$\therefore \mathrm{QR}=5 \mathrm{~m}$

Hence, the correct answer is option (d).