Choose the correct answer of the following question:
The length of the shadow of a tower standing on level ground is found to be 2x metres longer when the sun's elevation is 30° than when it was
45°. The height of the tower is
(a) $(2 \sqrt{3} x) \mathrm{m}$
(b) $(3 \sqrt{2} x) \mathrm{m}$
(c) $(\sqrt{3}-1) x \mathrm{~m}$
(d) $(\sqrt{3}+1) x \mathrm{~m}$
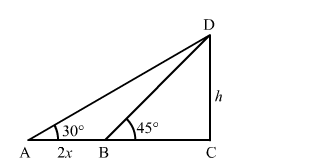
Let CD = h be the height of the tower.
We have,
$\mathrm{AB}=2 x, \angle \mathrm{DAC}=30^{\circ}$ and $\angle \mathrm{DBC}=45^{\circ}$
In $\Delta \mathrm{BCD}$,
$\tan 45^{\circ}=\frac{\mathrm{CD}}{\mathrm{BC}}$
$\Rightarrow 1=\frac{h}{\mathrm{BC}}$
$\Rightarrow \mathrm{BC}=h$
Now, in $\triangle \mathrm{ACD}$,
$\tan 30^{\circ}=\frac{\mathrm{CD}}{\mathrm{AC}}$
$\Rightarrow \frac{1}{\sqrt{3}}=\frac{h}{\mathrm{AB}+\mathrm{BC}}$
$\Rightarrow \frac{1}{\sqrt{3}}=\frac{h}{2 x+h}$
$\Rightarrow 2 x+h=h \sqrt{3}$
$\Rightarrow h \sqrt{3}-h=2 x$
$\Rightarrow h(\sqrt{3}-1)=2 x$
$\Rightarrow h=\frac{2 x}{(\sqrt{3}-1)} \times \frac{(\sqrt{3}+1)}{(\sqrt{3}+1)}$
$\Rightarrow h=\frac{2 x(\sqrt{3}+1)}{(3-1)}$
$\Rightarrow h=\frac{2 x(\sqrt{3}+1)}{2}$
$\therefore h=x(\sqrt{3}+1) \mathrm{m}$
Hence, the correct answer is option (d).
