Question.
Check whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial.
(i) $t^{2}-3,2 t^{4}+3 t^{3}-2 t^{2}-9 t-12$
(ii) $x^{2}+3 x+1,3 x^{4}+5 x^{3}-7 x^{2}+2 x+2$
(iii) $x^{3}-3 x+1, x^{5}-4 x^{3}+x^{2}+3 x+1$
Check whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial.
(i) $t^{2}-3,2 t^{4}+3 t^{3}-2 t^{2}-9 t-12$
(ii) $x^{2}+3 x+1,3 x^{4}+5 x^{3}-7 x^{2}+2 x+2$
(iii) $x^{3}-3 x+1, x^{5}-4 x^{3}+x^{2}+3 x+1$
Solution:
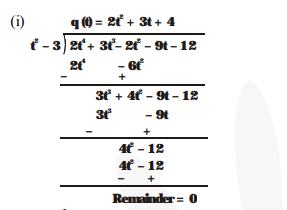
Hence, $t^{2}-3$ is a factor of
$2 t^{4}+3 t^{3}-2 t^{2}-9 t-12$
(ii) $x^{2}+3 x+1$
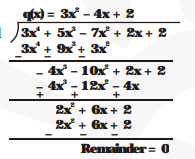
Hence, $x^{2}+3 x+1$ is a factor of
$3 x^{4}+5 x^{3}-7 x^{2}+2 x+2$
(iii) $x^{3}-3 x+1$
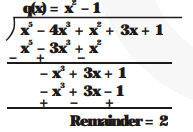
Hence, $x^{2}-3 x+1$ is not a factor of
$x^{5}-4 x^{3}+x^{2}+3 x+1$
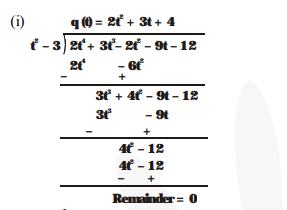
Hence, $t^{2}-3$ is a factor of
$2 t^{4}+3 t^{3}-2 t^{2}-9 t-12$
(ii) $x^{2}+3 x+1$
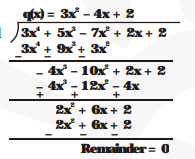
Hence, $x^{2}+3 x+1$ is a factor of
$3 x^{4}+5 x^{3}-7 x^{2}+2 x+2$
(iii) $x^{3}-3 x+1$
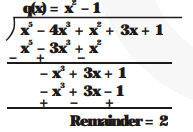
Hence, $x^{2}-3 x+1$ is not a factor of
$x^{5}-4 x^{3}+x^{2}+3 x+1$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.