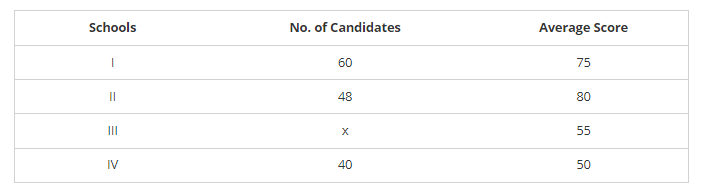
Candidates of four schools appear in a mathematics test. The data were as follows:

Given the average score of all schools = 66

$\Rightarrow \frac{\mathrm{N}_{1} \overline{\mathrm{x}}_{1}+\mathrm{N}_{2} \overline{\mathrm{x}}_{2}+\mathrm{N}_{3} \overline{\mathrm{x}}_{3}+\mathrm{N}_{4} \overline{\mathrm{x}}_{4}}{\mathrm{~N}_{1}+\mathrm{N}_{2}+\mathrm{N}_{3}+\mathrm{N}_{4}}=66$

$\Rightarrow \frac{60 \times 75+48 \times 80+x \times 55+40 \times 50}{60+48+x+40}=66$

$\Rightarrow \frac{4500+3840+55 x+2000}{148+x}=66$

$\Rightarrow \frac{10340+55 x}{148+x}=66$

⇒ 10340 + 55x = 66x + 9768

⇒ 10340 − 9768 = 66x − 55x

⇒ 11x = 572

⇒ x = 572/11 = 52

∴ No. of candidates appeared from school III = 52.