Calculate the value of x in each of the following figures.

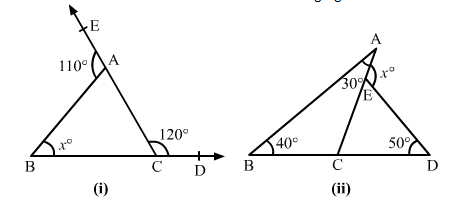
(i)

Side AC of triangle ABC is produced to E.

$\therefore \angle E A B=\angle B+\angle C$

$\Rightarrow 110^{\circ}=x+\angle C \quad \ldots(i)$

Also,

$\angle A C D+\angle A C B=180^{\circ} \quad$ [linear pair]

$\Rightarrow 120^{\circ}+\angle A C B=180^{\circ}$

$\Rightarrow \angle A C B=60^{\circ}$

$\Rightarrow \angle C=60^{\circ}$

Substituting the value of $\angle C$ in $(i)$, we get $x=50$

(ii)

From $\Delta A B C$ we have:

$\angle A+\angle B+\angle C=180^{\circ} \quad$ [Sum of the angles of a triangle]

$\Rightarrow 30^{\circ}+40^{\circ}+\angle C=180^{\circ}$

$\Rightarrow \angle C=110^{\circ}$

$\Rightarrow \angle A C B=110^{\circ}$

Also,

$\angle E C B+\angle E C D=180^{\circ} \quad$ [linear pair]

$\Rightarrow 110^{\circ}+\angle E C D=180^{\circ}$

$\Rightarrow \angle E C D=70^{\circ}$

Now, in $\Delta E C D$,

$\therefore \angle A E D=\angle E C D+\angle E D C \quad$ [exterior angle property]

$\Rightarrow x=70^{\circ}+50^{\circ}$

$\Rightarrow x=120^{\circ}$

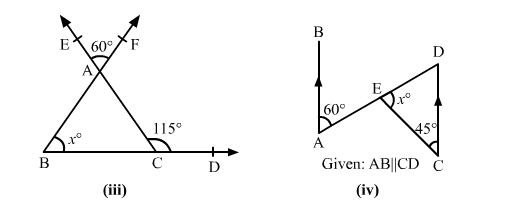
(iii)

$\angle A C B+\angle A C D=180^{\circ} \quad$ [linear pair]

$\Rightarrow \angle A C B+115^{\circ}=180^{\circ}$

$\Rightarrow \angle A C B=65^{\circ}$

Also,

$\angle E A F=\angle B A C \quad$ [Vertically-opposite angles]

$\Rightarrow \angle B A C=60^{\circ}$

$\therefore \angle B A C+\angle A B C+\angle A C B=180^{\circ} \quad$ [Sum of the angles of a triangle]

$\Rightarrow 60^{\circ}+x+65^{\circ}=180^{\circ}$

$\Rightarrow x=55^{\circ}$

(iv)

$\angle B A E=\angle C D E \quad$ [Alternate angles]

$\Rightarrow \angle C D E=60^{\circ}$

$\therefore \angle E C D+\angle C D E+\angle C E D=180^{\circ} \quad[$ Sum of the angles of a triangle $]$

$\Rightarrow 45^{\circ}+60^{\circ}+x=180^{\circ}$

$\Rightarrow x=75^{\circ}$

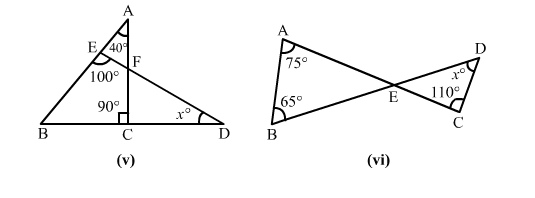
(v)

From $\Delta A B C$, we have:

$\angle B A C+\angle A B C+\angle A C B=180^{\circ} \quad$ [Sum of the angles of a triangle]

$\Rightarrow 40^{\circ}+\angle A B C+90^{\circ}=180^{\circ}$

$\Rightarrow \angle A B C=50^{\circ}$

Also, from $\Delta E B D$, we have:

$\angle B E D+\angle E B D+\angle B D E=180^{\circ} \quad$ [Sum of the angles of a triangle]

$\Rightarrow 100^{\circ}+50^{\circ}+x=180^{\circ} \quad[\because \angle A B C=\angle E B D]$

$\Rightarrow x=30^{\circ}$

(vi)

From $\Delta A B E$, we have:

$\angle B A E+\angle A B E+\angle A E B=180^{\circ} \quad$ [Sum of the angles of a triangle]

$\Rightarrow 75^{\circ}+65^{\circ}+\angle A E B=180^{\circ}$

$\Rightarrow \angle A E B=40^{\circ}$

$\therefore \angle A E B=\angle C E D \quad[$ Vertically-opposite angles $]$

$\Rightarrow 110^{\circ}+x+40^{\circ}=180^{\circ}$

$\Rightarrow x=30^{\circ}$