Calculate the mean deviation about median age for the age distribution of 100 persons given below:

The given data is not continuous. Therefore, it has to be converted into continuous frequency distribution by subtracting 0.5 from the lower limit and adding 0.5 to the upper limit of each class interval.

The table is formed as follows.

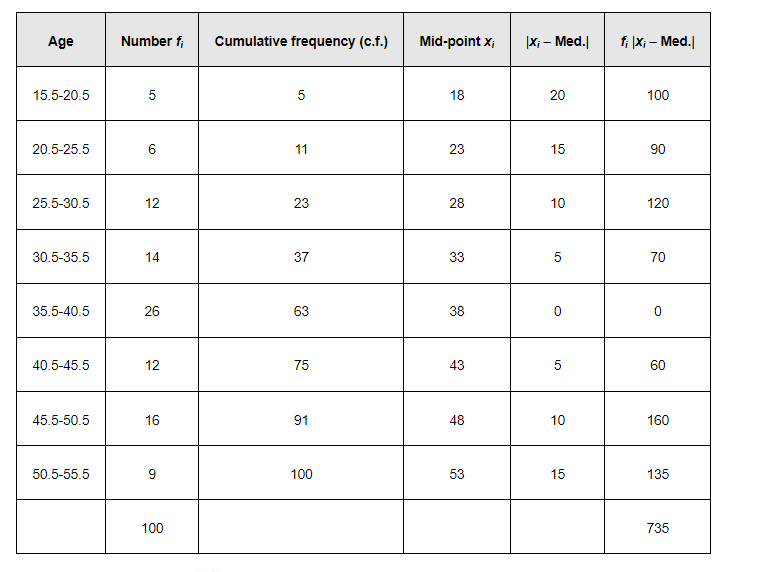
The class interval containing the $\frac{\mathrm{N}^{\text {th }}}{2}$ or $50^{\text {th }}$ item is $35.5-40.5$.

Therefore, 35.5 – 40.5 is the median class.

It is known that,

Median $=l+\frac{\frac{\mathrm{N}}{2}-\mathrm{C}}{f} \times h$

Here, $I=35.5, C=37, f=26, h=5$, and $N=100$

$\therefore$ Median $=35.5+\frac{50-37}{26} \times 5=35.5+\frac{13 \times 5}{26}=35.5+2.5=38$

Thus, mean deviation about the median is given by,

M.D. $(\mathrm{M})=\frac{1}{\mathrm{~N}} \sum_{i=1}^{8} f_{i}\left|x_{i}-\mathrm{M}\right|=\frac{1}{100} \times 735=7.35$