Calculate the height of an equilateral triangle each of whose sides measures 12 cm.

We are asked to find the height of the equilateral triangle.

Let us draw the figure. Let us draw the altitude AD. We know that altitude is also median of the equilateral triangle.

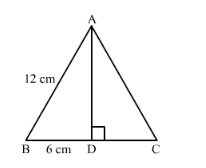
Therefore, $B D=D C=6 \mathrm{~cm}$

In right angled triangle ADB, we will Pythagoras theorem, as shown below,

$A B^{2}=A D^{2}+B D^{2}$

Now we will substitute the values.

$12^{2}=A D^{2}+6^{2}$

$144=A D^{2}+36$

$A D^{2}=144-36=108$

Taking square root, we get

$A D=10.39 \mathrm{~cm}$

Therefore, the height of the equilateral triangle is $10.39 \mathrm{~cm}$.