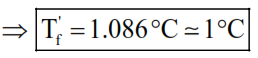$\mathrm{C}_{6} \mathrm{H}_{6}$ freezes at $5.5^{\circ} \mathrm{C}$. The temperature at which a solution $10 \mathrm{~g}$ of $\mathrm{C}_{4} \mathrm{H}_{10}$ in $200 \mathrm{~g}$ of $\mathrm{C}_{6} \mathrm{H}_{6}$ freeze is ${ }^{\circ} \mathrm{C}$. (The molal freezing point depression constant of $\mathrm{C}_{6} \mathrm{H}_{6}$ is $5.12^{\circ} \mathrm{C} / \mathrm{m}$.)
Pure Solvent : $\mathrm{C}_{6} \mathrm{H}_{6}(\ell)$
Given : $\mathrm{T}_{\mathrm{f}}^{\circ}=5.5^{\circ} \mathrm{C}$
$\mathrm{K}_{\mathrm{f}}=5.12^{\circ} \mathrm{C} / \mathrm{m}$

$\because \Delta \mathrm{T}_{\mathrm{f}}=\mathrm{k}_{\mathrm{f}} \times \mathrm{m}$
$\Rightarrow\left(\mathrm{T}_{\mathrm{f}}^{0}-\mathrm{T}_{\mathrm{f}}^{\prime}=5\right) \cdot 12 \times \frac{\left(\frac{10}{58}\right)}{\left(\frac{200}{1000}\right) \mathrm{kg}} \mathrm{mol}$
$\Rightarrow 5.5-\mathrm{T}_{\mathrm{f}}^{\prime}=\frac{5.12 \times 5 \times 10}{58}$