Question:
By actual division, show that $x^{2}-3$ is a factor of $2 x^{4}+3 x^{3}-2 x^{2}-9 x-12$
Solution:
Let $f(x)=2 x^{4}+3 x^{3}-2 x^{2}-9 x-12$ and $g(x)=x^{2}-3$
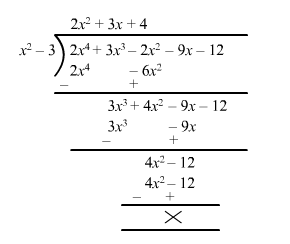
Quotient $q(x)=2 x^{2}+3 x+4$
Remainder $r(x)=0$
Since, the remainder is 0 .
Hence, $x^{2}-3$ is a factor of $2 x^{4}+3 x^{3}-2 x^{2}-9 x-12$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.